Here’s an open discussion thread for you…
The other day I saw this image and posted it on my Tumblelog, with the comment “Not sure how to take this”.
Anyways, it ended up being extremely popular amongst the tumblr crowd with a lot of people reposting it and linking to it and “liking” it (a tumblr thing).
My question is: Why?
Why do you think so many people found this image worth sharing?
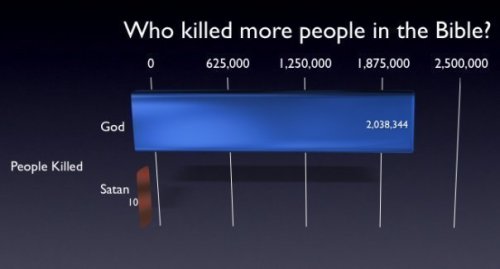
I wouldn't know, but those figures are surely wrong…
Satan killed *ten* people? I find that hard to believe. Can't remember anyone; maybe I should read the Bible looking for people Satan killed. Anyway, my claim is — that figure of ten must be highly inflated.
Also, I'd say move those ten to God — if Satan ever kills anyone it's because God lets it kill. So God is the Giver and Taker of all life.
God ever forbid that Satan would take my life. Whereas if God themselves wants to snap their fingers my way, well, I claim my life is theirs so they'd actually not be taking anything that's not theirs already.
Why do so many like that image? – I'd like to ask why the image was created and what were he motives behind it?
During the time i was not a Christian one of the biggest issues i had was of how Guilty i felt about stuff to do with God. Being brought up catholic the attitude i developed was one of guilt and shame which is such a common view.
Developing on from this when one is cornered or made to feel guilty or shameful, the "knee jerk" reaction is to push the blame on someone else. This can then go on and develop in to anger and even resentment. At least it did for me.
When I got to this stage i started to blame God for everything. It was easy to say that i didn't want any part of a God that killed races of people because it felt like i was giving myself the higher ground morally.
I think a lot of people are angry. They look for excuses to blame stuff on God because they don’t want to be accountable. Being accountable men that someone else knows of those "dirty little secrets" – this can feed the "shame – guilt – anger – resentment – blame " circle even more. When this happens those arguments that one has developed becomes even more complex – another link is addend to the armour.
So why do so many like that image? – "shame – guilt – anger – resentment – blame " all driven by someone who wants to makes us think he doesn't exist – Satan.
ON THE OTHER HAND.
I do look at this and say – "what is the context?" I'm sure that biblically speaking there are as few deaths directly attributed to Satan. BUT – what has happened since Jesus died on the cross has reversed that in a huge way.
This is a really big discussion and my meagre typing can’t get down what i wanna say so I’ll stop here.
Spread the love
@irishmark: Your mention of a guilt trip and Christianity evoked something I read a long time ago: Archbishop Rowan William's enthronement sermon, back in 2003. it begins:
"It's sometimes been said that if someone came up to you in the street and whispered, 'They've found out! Run!', nine out of ten of us would. We nearly all have secrets that we don't want exposed"
Reading that dropped my jaw abck then, and I'm marking it for a re-read: http://www.archbishopofcanterbury.org/842
Tintazul,
I appreciate your comment. However, I think a great many people don't think God is the "Giver and Taker of all life," but they have heard of enough Bible stories like Noah's Ark and others were God wipes out entire populations. They don't see it the same way you do, and I guess I'm thinking the perspective is very different for those who don't have your world view.
Mark, thank you for sharing your thoughts and a bit of your testimony. I believe your feelings and experiences are probably accurate for many others as well.
Personally, as a person whose considered myself a 'christian' for quite some time, I find the graph equally intriguing, but I feel like it's for a different reason.
You see, when I was young, learning and growing in my faith in the church, we never dealt with things like this. The reality is that on a face value read of the Old Testament, God wiped out a lot of people. If we, in the church, haven't talked about or wrestled with that to any real degree, well then I think it's valid for those outside the faith to raise the same sort of questions and critiques.
Neither have I heard clear explanations for that growing up. I suspect many Bible teachers don't know enough to deal with that, and also that there's a sentimental mood in many Evangelical churches which actively discourages that kind of thinking.
If us Christians' theology were half good, we shouldn't be amazed at the deaths, and we'd have some explanations. For instance, the Israelites were commanded to totally wipe out the peoples of Canaan (which they didn't.) Yet, God waited for 400 years, since he'd told Abraham in Genesis 15.16, "In the fourth generation your descendants will come back here, for the sin of the Amorites has not yet reached its full measure." So, from a single passage we learn it takes a full measure of collective sin for God to order that kind of wipeout. Also that the Jews had to wait 400 years (and be enslaved by the Egyptians) precisely because of God's patience with the canaanites.
Reading the Old Testament reveals a God who will not tolerate gross idolatry in the face of knowledge of him, but who warns people way in advance and who is slow to anger. A scholar I read (Walter Kaiser, "The Hard Sayings of the Old Testament") suggests that the greatest of all collective sins was people routinely sacrificing their own children to Moloch. Can non-believers imagine that? How many non-christians would revolt against such a thing? Well, God did. Keep reading Genesis — they had knowledge of Yahweh; see Genesis 21.22-34 where the king of the Amalekites makes a treaty with Abraham. Hardly innocent.
An even simpler example: Jonah and the Ninivites. God spares 120 thousand people in one sweep of his mercy. If God wanted the destruction of Nineveh, why talk about it? A flick of God's wrist, as it were, would be enough. But God didn't want annihilation — he wanted repentance. And we're talking about some of the most brutal people recorded in the Old Testament — they wiped out the Northern Kingdom.
How about the Jews themselves? I would think most of those 2 million dead would be Jews. We have whole books of the Bible where God told his people to repent, don't go the way of the Canaanites, don't worship the baby-hungry Moloch, Aseraph and such lot. Practise mercy, have Jubilees. But no. First the Northern Kingdom and then the Southern were taken away. Jeremiah spent his whole life talking to those who would not listen. Results? The Kingdom of Judah was deported to Babylon, but — very importantly — the idolatry ended there. Amazingly, we don't see idolatry among the Jews in Jesus' time. God is good.
Of course we will never know all that if we stick to a sentimental status quo which equates "worship" with songs and not to applying our whole minds to the whole Word of God.
I like yor thinking – i wanted t go into that side of things but dont have the time, hence my eding it abruptly but you are right – there are a lot more layers to this – am supposed to be working;)
You are right, I am writing to burn Christian ears 🙂 (including my own.) Non-Christians wouldn't see it as I do, but yet I stick to my guns: those figures are wrong, man. A few players are missing: add an entry for
Four angels of Revelation 9.15: 2,255,952,725
One-third of the population, current figures from http://www.census.gov/ipc/www/popclockworld.html. A thousand times God's figure. That should balance things. 🙂
This image is popular because the majority of the tumblr user base is secular. Oh and it's easy to make fun of religion. Kind of like shooting fish in a barrel.
Daelan,
thanks for joining the conversation. I definitely realize the majority of the tumblr base is 'secular', but I guess I'm still curious why they find this image worth sharing.
More then just making fun of religion…
I agree
On a side note…they're not exactly equal beings, I'm pretty sure Satan would more than equal things out, given the opportunity
I agree
On a side note…they're not exactly equal beings, I'm pretty sure Satan would more than equal things out, given the opportunity
People who aren't religious love pointing out the absurd nature of religion. When something is shown to you that reinforces a point of view that you share you are going to like it and you will want to share it with like minded people.
I think it's because it and makes you think about the phrase "God is good." People like that image who are skeptics and who have a gut reaction that says, "yeah, this validates my thoughts." Plus, no matter what you think about the image, it's sort of funny because it makes you think, well how many people does God kill in the bible because the means justify the end? These figures are pretty suspect, but I sure would be interested to see some serious analysis of that question.
Because murder is the ultimate wrong in human culture, and power over life is the ultimate authority. And the idea of a God who can and will say when people will die is scary. Also, people don't make the distinction between the "when" people will die, and the "if" people will die.
And anyway, why would the devil be trying to kill us? I would suspect that he's way more interested in having us live and perpetuate evil, injustice and oppression, and raise our children in evil, unjust, and oppressive ways than in having us die quickly.
I think the 10 were Job's 10 children whom Satan killed to see if Job would turn against God.
Great point about the devil not necessarily wanting to kill us. I
think that's a conversation, just the idea of death being the ultimate
wrong and tragedy.
There's a Bible expert in our midst! Well done Zach.
It's an unsourced statement, so all we can have hunches about who's who, and gut reactions to it. Unless someone knows where the data come from? There has to be something out there.
I think the graph might have been based on this http://dwindlinginunbelief.blogspot.com/2006/08/h… or something similar.
Wow, that's a great chart on the link, and proves the graph
surprisingly accurate, even a bit modest.
Tintazul,
decent point, but I'm not sure a crowd already skeptical of the current story as it's told is going to believe future predictions either. Those who do believe probably aren't interested in the competition thing anyways.
Great point about the devil not necessarily wanting to kill us. I
think that's a conversation, just the idea of death being the ultimate
wrong and tragedy.
Lisa, great thoughts. I think your right on about it challenging the idea of God being good.
Did you see Zach's link about the figures? They seem pretty accurate actually.
Well it is entirely true, and quite an interesting fact. God was the most brutal dude in history back then.
…Devil not wanting to kill us, _unless_ he really believes in redemption — that God can pick up any of us and make something new and wonderful at any time, if we give him half a chance. If that be the case, than death would be Satan's plan A for every human being. Just to be on the safe side.
When Jesus told the repentant robber on the cross, "Today you will be with me in paradise", I bet Satan went, "Blimey, pipped at the post!" (if he speaks with a British accent.) A lifetime of doing his eeevil with the robber's life, and now the guy's just… saved by the Saviour. Not fair on Old Nick. Mwa ha hah!
hey Ariah, i need to get more internet savvy.
what is the purpose of the additional tumblr blog? and do you twitter?
i picked up your book btw, but havn't read it yet i'll let you know when i do
w0rm@hotmail.com
I don't like disputing figures, and yes the guy who did the counting seems to be taking it methodically. We could look into God's motives, though, and also how many he spared after he warned them of their impending destruction. Jonah 4 is quite surprising for me because God's prophet did not want God to be merciful but actually wanted him to wipe out all of the city, and God tells Jonah, "can't you feel for 120 thousand people, and even their animals?" If someone ever needed to rethink their career options, Jonah did.
I wouldn't know about who was the most brutal back then, since I've never studied enough ancient history. If you want to say God was, I'd go so far as to say that's an unsourced statement but I wouldn't refute it (I don't like refuting people's arguments.) I would instead put that figure of 2,2 million in a broader context.
Think World War II: 50 million died because of the greed, racism and even idiocy of a handful of humans. Russia had the most casualties: 20 million. Six million Jews. Even the "good guys" look very bad, read up on the bombing of Dresden or Hiroshima/Nagasaki.
So, balance these two: God calling the shots in a few hundred years produced 2,2 million dead; humans calling the shots in six years produced 50 million dead. So, if you think a good God should do better than humans, well — he is already doing better. You might now want to look into the motives behind God's killings, get inside the "Big Killer's mind" if you will. Or not; either way I'd respect you and your opinion.
The issue of life being God's to give and take has already been talked about, and I want to say a little more about it. I think that we simply can't judge God by human standards, and this is really important for at least two reasons: 1) if we do so, we'll never fully embrace the biblical revelation of God's sovereignty and judgment, and 2) if we don't separate God from our standards, then we seem to be prone to deifying our standards. (I'm thinking of some of the rhetoric I've heard and read from my fellow pacifists…)